階層モデルでロバストな推定を試す
【追記】
「外れ値の確認」の項目を追記しました。
以前『データ分析をマスターする〜』の9章を階層モデルを使って分析しました。しかし,ちょっと気になることがあったので,再分析してみます。なお,本エントリーは Stan Advent Calendar 2017 の9日目です。
今回主に使うパッケージは次の2つです。
library(tidyverse) library(brms) library(rethinking) # devtools::install_github("rmcelreath/rethinking",ref="Experimental") # 必要であれば。
使用したデータは『データ分析をマスターする〜』のサポートサイトにありますが,使って見るならちゃんと買ったほうがいいかなぁと思います(私は買って読んでます)。
以前の分析の課題 〜外れ値の存在〜
この前は都道府県別の女性労働力率と合計特殊出生率のデータを使って,シンプソンのパラドックスをベイズ推定を使った階層モデル(マルチレベル分析)でどう解消するか考えました。↓がこの前のエントリーです。
データの特徴は「全体で見ると負の相関だけど,年代別(1980年と2000年)で見ると正の相関が出る」というものです。散布図を再掲します。
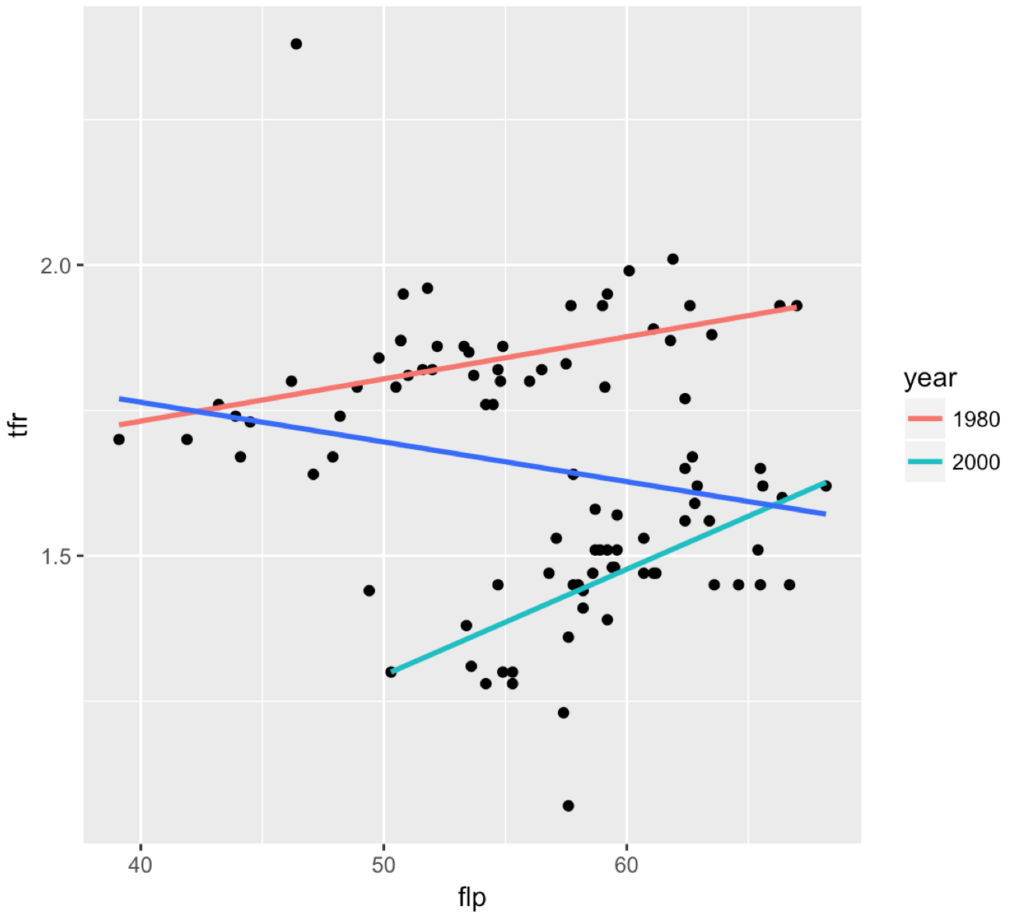
前回,傾きはほぼ同じだから,変量効果は切片だけ考えました。それはいいのですが,気になっていて見なかったことにしようとしたことが1つ。外れ値の存在です。
ggplot(d, aes(x=factor(year), y=tfr)) + geom_boxplot(aes(fill=factor(year))) + geom_jitter() + coord_flip() + theme(legend.position = "none")
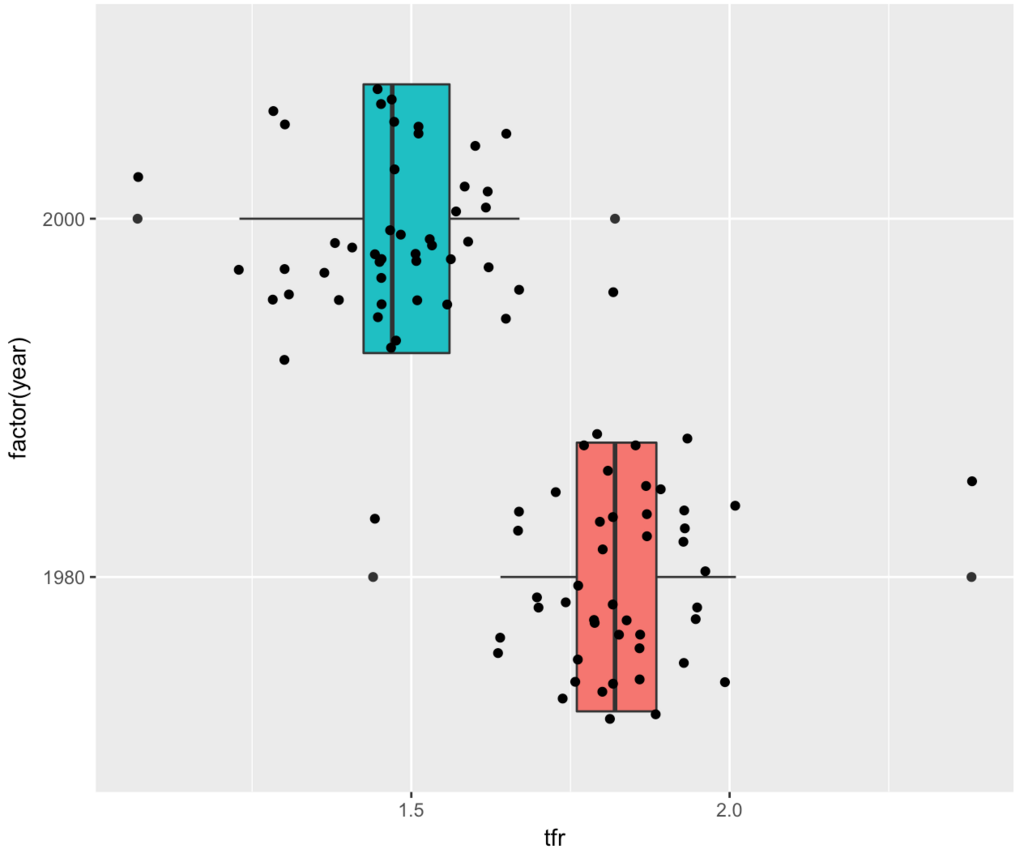
上図を見ると,各年代で合計特殊出生率の極端に高い都道府県と極端に低い都道府県が存在します。下表から、どの年代も最大値は沖縄(都道府県コード47)で,最小値は東京都(都道府県コード13)です。
library(knitr) # kable() で下の表を作るためにマークダウン出力用 d %>% group_by(year) %>% summarise(max(tfr), which.max(tfr), min(tfr), which.min(tfr)) %>% kable()
| year | min(tfr) | which.min(tfr) | max(tfr) | which.max(tfr) |
|---|---|---|---|---|
| 1980 | 1.44 | 13 | 2.38 | 47 |
| 2000 | 1.07 | 13 | 1.82 | 47 |
外れ値の確認
外れ値が存在するときは t 分布を使うとよいと犬4匹本に書いてあります(466ページ)ので,以下,t分布を使った外れ値があるデータにも対応できるロバストな分析を行います。
ところで、今回のケースが外れ値といえるのか少し確かめたいと思います。外れ値を調べるために Smirnov-Grubbs 検定(すみるのふぐらぶす)があります。この検定はデータが正規分布から発生している仮定しています。しかし、今回はt分布から発生すると考えていきたいので、自由度46(=47-1)のt分布の95%信頼区間を見て判断してみます。
t = abs(qt(0.05/2, 47-1)) SE1980 = sd(d$tfr[d$yearID==1])/sqrt(47) SE2000 = sd(d$tfr[d$yearID==2])/sqrt(47) > # 1980年の下側 > mean(d$tfr[d$yearID==1]) - t*SE1980 [1] 1.789009 > # 1980年の上側 > mean(d$tfr[d$yearID==1]) + t*SE1980 [1] 1.868012 > # 2000年の下側 > mean(d$tfr[d$yearID==2]) - t*SE2000 [1] 1.433888 > # 2000年の上側 > mean(d$tfr[d$yearID==2]) + t*SE2000 [1] 1.512069
1980年の95%信頼区間は1.79〜1.87,2000年の95%信頼区間は1.43〜1.51でした。よって,外れ値が存在すると言えそうです。上記の計算はこちらを参考にしました。
t 分布を使ったロバストな推定
ロバストとは?
ロバストとは「頑健」という意味です。外れ値があっても,データのメインボディの中心やばらつきなどを妥当に推定する方法を「ロバスト推定」と言います(藤澤 2017)。
t分布には3つのパラメータがあります。自由度ν(にゅー),中心μ(みゅー),スケールσ(しぐま)です。μやσは平均と標準偏差の記号として使われますが,ここではt分布なので平均ではなく中心 center,標準偏差ではなくスケール scale と書きました(BDA3, 437ページ)。
t 分布の感じをつかむには Unadon さんのこちらのエントリーがわかりやすいです。
Stan のおすすめ事前分布を見ると,t(3, 0, 1)のようですが,上の箱ひげ図を見ると幅広そうなので,今回はできるだけ幅が広く,裾が長いt分布の t(1, 0, 10)でやってみます。なお,BDA3には「自由度が1や2のt分布はあんまり現実的ではない」とありますが,今回は実験ということで目をつぶります(437ページ)。
Stan おすすめ事前分布についてはこちらの説明があります。
Stan のコードは自前では書けませんので,今回も brms パッケージを使います。変量効果は前と同じ(半コーシー分布に従っている)。単回帰分析なので,切片とflpの傾きがt分布に従っていると考えます。モデルのイメージは下のような感じ(かっこいいグラフィカルな表現はできなかった)。
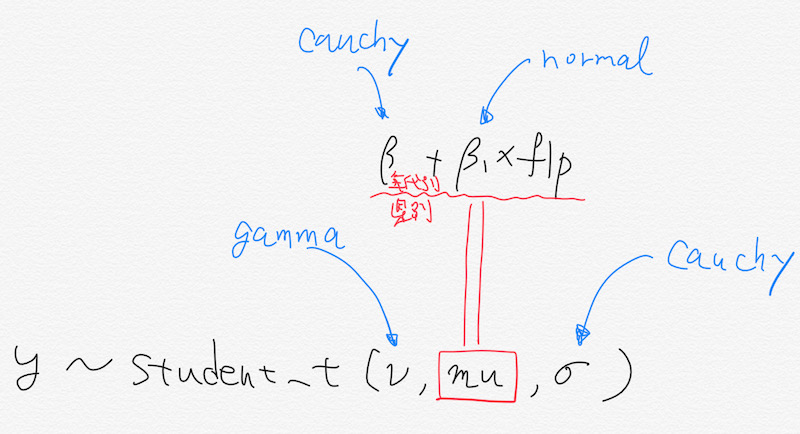
コードは次のとおりです。
library(brms) options(mc.cores = parallel::detectCores()) prior2 = c(set_prior("cauchy(0, 3)", class = "sd", group = "prefID"), set_prior("cauchy(0, 3)", class = "sd", group = "yearID"), set_prior("student_t(1,0,10)", class = "b"), set_prior("student_t(1,0,10)", class = "Intercept")) kekka2 = brm(tfr ~ 1 + flp + (1 | prefID) + (1 | yearID), data = d, iter = 5000, family = "student", prior = prior2, control = list(adapt_delta = 0.9, max_treedepth = 15))
ちゃんと指定した事前分布になっているかコードを確認します。
> stancode(kekka2) (中略) // priors including all constants target += student_t_lpdf(b | 1,0,10); ←ココ target += student_t_lpdf(temp_Intercept | 1,0,10); ←ココ target += student_t_lpdf(sigma | 3, 0, 10) - 1 * student_t_lccdf(0 | 3, 0, 10); target += gamma_lpdf(nu | 2, 0.1) - 1 * gamma_lccdf(1 | 2, 0.1); target += cauchy_lpdf(sd_1 | 0, 3) ←ココ - 1 * cauchy_lccdf(0 | 0, 3); target += normal_lpdf(z_1[1] | 0, 1); target += cauchy_lpdf(sd_2 | 0, 3) ←ココ - 1 * cauchy_lccdf(0 | 0, 3); target += normal_lpdf(z_2[1] | 0, 1); (後略)
分析結果
分析結果は次のとおりです。無事収束して,心なしか有効サンプルサイズが増えたようです。また前回と違って切片の固定効果は0をまたがなくなり,最後の警告の数は減りました。都道府県の変量効果と傾きの固定効果がほぼ0なのは同じです。
> kekka2 Family: student(identity) Formula: tfr ~ 1 + flp + (1 | prefID) + (1 | yearID) Data: d (Number of observations: 94) Samples: 4 chains, each with iter = 5000; warmup = 2500; thin = 1; total post-warmup samples = 10000 ICs: LOO = NA; WAIC = NA; R2 = NA Group-Level Effects: ~prefID (Number of levels: 47) Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sd(Intercept) 0.13 0.02 0.09 0.17 1183 1.01 ~yearID (Number of levels: 2) Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sd(Intercept) 0.96 0.82 0.15 3.11 1162 1.00 Population-Level Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept 1.67 0.69 0.22 3.16 1287 1.00 flp -0.00 0.00 -0.01 0.01 829 1.00 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sigma 0.04 0.01 0.03 0.05 1538 1.00 nu 13.89 11.73 2.69 46.47 5153 1.00 Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1). 警告メッセージ: There were 7 divergent transitions after warmup. Increasing adapt_delta above 0.9 may help. See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup >
警告メッセージについては,divergent transitions の数が小さいのと Rhat を見ると収束しているので無視します(アヒル本176ページ)。
傾きは前回と同じように変量効果も固定効果も0に近いです。切片の変量効果が減ってしまっています(前のモデルが1.22)が,切片の固定効果の95%信用区間は0をまたがなくなりました(切片の有効サンプルサイズも増えています)。図で確認します(太い線が50%信用区間,細い線が90%信用区間です。点は事後中央値)。
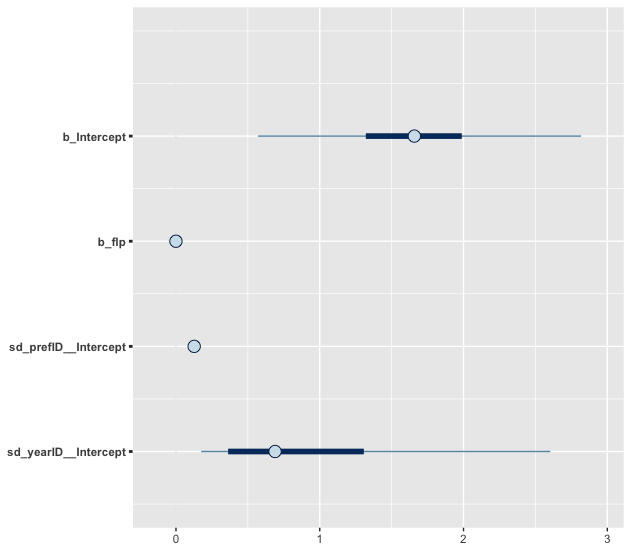
モデル比較
WAIC は前回のモデルに及びませんでした。残念。
> waic(kekka1, kekka2) WAIC SE kekka1 -268.04 16.62 kekka2 -260.81 18.53 kekka1 - kekka2 -7.23 3.47
まとめ
今回は「外れ値があるので,ロバストな推定をしよう」とチャレンジしてきました。結果はイマイチで,たった94行のデータに適用するのはあんまり意味がないのでしょう。しかし,いつもと違った事前分布に触れることができました。また Stan コードが書けなくても,パッケージで比較的に Stan に触れられる例にもなったかなと思います。
間違いなどがあれば,ぜひお教えください🙏
いつかお会いする機会があれば🍣を進呈いたします。
参考にした書籍
以下,今回,参考にした書籍です。どれも難しいですね…。

データ分析をマスターする12のレッスン (有斐閣アルマBasic)
- 作者: 畑農鋭矢,水落正明
- 出版社/メーカー: 有斐閣
- 発売日: 2017/10/12
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る

ロバスト統計: 外れ値への対処の仕方 (ISMシリーズ:進化する統計数理)
- 作者: 藤澤洋徳
- 出版社/メーカー: 近代科学社
- 発売日: 2017/07/31
- メディア: 単行本
- この商品を含むブログを見る

ベイズ統計モデリング: R,JAGS, Stanによるチュートリアル 原著第2版
- 作者: John K. Kruschke,前田和寛,小杉考司
- 出版社/メーカー: 共立出版
- 発売日: 2017/07/22
- メディア: 大型本
- この商品を含むブログを見る

StanとRでベイズ統計モデリング (Wonderful R)
- 作者: 松浦健太郎,石田基広
- 出版社/メーカー: 共立出版
- 発売日: 2016/10/25
- メディア: 単行本
- この商品を含むブログ (8件) を見る

Bayesian Data Analysis, Third Edition (Chapman & Hall/CRC Texts in Statistical Science)
- 作者: Andrew Gelman,John B. Carlin,Hal S. Stern,David B. Dunson,Aki Vehtari,Donald B. Rubin
- 出版社/メーカー: Chapman and Hall/CRC
- 発売日: 2013/11/05
- メディア: ハードカバー
- この商品を含むブログを見る

- 作者: Richard McElreath
- 出版社/メーカー: Chapman and Hall/CRC
- 発売日: 2016/02/19
- メディア: ハードカバー
- この商品を含むブログを見る
RStudio Cloud による社会人学生への統計教育の実践
Hijiyama.R the Final で LT をしてきました。LT のタイトルは「RStudio Cloud による社会人学生への統計教育の実践」です。RStudio Cloud を使えば,みんな同じ環境でRに触れることができるよ,という内容でした。

月1ペースで社会人学生で統計分析の勉強会をしているのですが,次のような理由で分析する環境を整えるのが結構大変だと思っていました。
PC環境がバラバラで環境構築であきらめることも。
アカウント名が日本語になっていることがよくある。
RStudioやパッケージを全員がちゃんとインストールするのが難しい…。
一人ひとりフォローすればなんてことはないのですが,勉強会は月1で1時間程度で時間がないのです。どうしたもんかと悩んでいたところに救世主が!

使い方はとても簡単。右上の Login から「Log in with Google」で利用できるようになります。ログイン後,しばらく待っているとスタンバイ完了。New Project でプロジェクトを作って,いつものようにRStudioを使うだけ。

動作は重いです。データは右下のペインの「Upload」からアップします。R スクリプトを書いて保存して,URLを共有すれば,すぐに他の人も使えます。違うアカウントでログインすると,右下に作成したスクリプトやデータがありますし,共有前にパッケージをインストールしていたら,そのパッケージも使えます(しかし,rstan とはダメです)。

まとめ
- R を使ってこんなふうに分析できるよという紹介用レベルには使える。
- 重い。
以上です。
補足
kazutan 先生によれば,次のとおりだそうです。
んー、これalpha版で多分test期間中なはず。
— kazutan v3.4.2 (@kazutan) 2017年11月26日
補足2
今日はいつもと違って,Jupyter Notebook + RISE でプレゼンしました。

経営学における階層モデルの使われ方
2017年10月28日 関大梅田キャンパス Kandai MeRise で Kobe.R annex(犬4匹本輪読会)第2回を開催しました! 参加者は3名でした。対象となったのは『ベイズ統計モデリング』通称・犬4匹本の第9章と10章。

ベイズ統計モデリング: R,JAGS, Stanによるチュートリアル 原著第2版
- 作者: John K. Kruschke,前田和寛,小杉考司
- 出版社/メーカー: 共立出版
- 発売日: 2017/07/22
- メディア: 大型本
- この商品を含むブログを見る
難しいです。懇切丁寧なのは確かですが,難しいです・・・。両章ともテーマは階層モデリングでした。参加者の方から9章の内容が報告されました。私のほうは10章はさておき,「経営学における階層モデルの使われ方」というテーマで発表を行いました。

内容は『組織科学』Vol.44 No.4 「マルチレベル分析への招待」をネタにしたものです。経営学では,まずマルチレベル分析は見ないです。その中で貴重な特集号となっています。犬4匹本は階層ベイズですが,この『組織科学』の特集はベイズ推定は使われていません。マルチレベル分析がこんなふうに使われてるよ,と経営学ではない人向けへの発表です。

なお,この特集号は全文PDFで読めます。興味がある方は↓のリンクをたどってください。
http://www.aaos.or.jp/contents/committee/?page=184
Kobe.R annex 第3回は2017年12月を予定しています。ご案内は↓で行っています。
シンプソンのパラドックスと階層ベイズ
丸の内オアゾに入っている書店をぶらついているときに『データ分析をマスターする12のレッスン』という本を見つけました。最近出た学部3〜4年生向けの本のようです。パラパラと立ち読みしたところ,商学と政策の先生が書いた本で自分にちょうどよさそうなレベルだったのでお買い上げ。

データ分析をマスターする12のレッスン (有斐閣アルマBasic)
- 作者: 畑農鋭矢,水落正明
- 出版社/メーカー: 有斐閣
- 発売日: 2017/10/12
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る
その中で,おもしろい例題がありました。各都道府県の合計特殊出生率と女性労働力率の関係です。グーグルによると,それぞれ次のとおりです。
合計特殊出生率(tfr):一人の女性が一生に産む子供の平均数
女性労働力率(flp): 15歳以上の女性の人口に占める、実際に働いている、もしくは求職中の女性の割合。
横軸を女性労働力率,縦軸を合計特殊出生率でプロットすると,次のようになります。

散布図を見る限り,負の相関があります。実際に相関係数は -0.19。しかし,このデータは1980年と2000年のデータがいっしょになっていて,年代を色分けし,回帰直線を引いてみると次のようになります。青い回帰直線は年代別にしなかった場合のもの。

全体と層別にしたときに結果が異なるシンプソンのパラドックスが起きています。層別にすると,女性労働力率が大きいほど合計特殊出生率が大きくなって「女性が働くほど子どもが生まれやすい」なんて説明がつきそうです。
『データ分析をマスターする12のレッスン』ではトレンド項というのを入れたりして,うまく解決していくのですが,年代でネストされていて,都道府県の個別事情(効果)も踏まえたマルチレベル分析でもやれるのではないかと思い,練習がてら,やってみることにしました。
ベイズ推定でやる! ちょうど犬4匹本の輪読会も開催するし
各都道府県の年代別で線を引いてみると,そんなに傾きは変わらないようなので,ランダム切片だけに絞ります。

このレベルの Stan コードはまだ自前で書けないので,brms パッケージ頼み 。
prior = c(set_prior("cauchy(0, 3)", class = "sd", group = "prefID"), set_prior("cauchy(0, 3)", class = "sd", group = "yearID")) library(brms) kekka.1 = brm(tfr ~ 1 + flp + (1 | prefID) + (1 | yearID), data = d, iter = 5000, prior = prior, control = list(adapt_delta = 0.9, max_treedepth = 12))
上段はランダム切片の事前分布です。この事前分布にしたのは,stan レファレンスマニュアル(日本語版)を参考にして設定しました。もっといい設定があれば教えてください。下段がベイズ推定をしているところ。control の部分はオプションです。実行すると次のようなエラーが出ます。アドバイスに従って,最大値まで上げても消えなかったので,まあまあの落としどころとして設定しました。
警告メッセージ: There were ●●●● divergent transitions after warmup. Increasing adapt_delta above 0.9 may help. See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
推定結果
次のとおりで,Rhat だけで判断すると収束しています(有効サンプルサイズは気にしなくていいかな?)。
> kekka.1 Family: gaussian(identity) Formula: tfr ~ 1 + flp + (1 | prefID) + (1 | yearID) Data: d (Number of observations: 94) Samples: 4 chains, each with iter = 5000; warmup = 2500; thin = 1; total post-warmup samples = 10000 ICs: LOO = NA; WAIC = NA; R2 = NA Group-Level Effects: ~prefID (Number of levels: 47) Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sd(Intercept) 0.13 0.02 0.10 0.17 1232 1.00 ~yearID (Number of levels: 2) Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sd(Intercept) 1.22 1.21 0.15 4.48 953 1.01 Population-Level Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept 1.69 1.09 -0.77 4.10 634 1.01 flp -0.00 0.00 -0.01 0.01 1095 1.00 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sigma 0.05 0.01 0.04 0.06 1590 1.00 Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1). 警告メッセージ: There were 402 divergent transitions after warmup. Increasing adapt_delta above 0.9 may help. See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
固定効果(Population-Level Effects)を確認すると,傾きはほぼゼロ。切片のランダム効果を見ると,都道府県別の効果(~prefID)は0.13。年代による効果(~yearID )は1.22で,年代による影響が多いとわかります。この点推定値は事後平均です。
図示するとこんな感じです。b_Intercept は固定効果の切片で,sd_yearID_Intercept は年代による切片のランダム効果です。b_Intercept の95%信用区間が0をまたいでいますが,事後平均値も事後最大値も0にはなっていないので,大きな問題はないかと思います。

こちらの図のほうが見やすいでしょうか(個人的には上のほうが好き)。太い線が50%信用区間,細い線が90%信用区間です。点は事後中央値。

以上,階層ベイズモデルによる結果を見ると「(このデータだけを使うと)女性労働力率があがると合計特殊出生率も上がるという関係はなく,都道府県による違いも小さく,時代の変化によって合計特殊出生率は下がっている」と言えそうです。
いい練習になるので,また『データ分析をマスターする12のレッスン』をネタにするかもしれません。
P.S.1
divergent transitions after warmup はどうしてもなくなっていないので,分析結果の妥当性がバッチリあるとは言えなさそうです。このエラーは階層モデルのときに起こりやすいみたい。推定するパラメータとデータの数が釣り合わないのかな・・・?
P.S.2
Mplus を使ってマルチレベルSEM&ベイズ推定もやってみようと思いましたが,やり方がわかりませんでした・・・。
今回,参考にした本

データ分析をマスターする12のレッスン (有斐閣アルマBasic)
- 作者: 畑農鋭矢,水落正明
- 出版社/メーカー: 有斐閣
- 発売日: 2017/10/12
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る

ベイズ統計モデリング: R,JAGS, Stanによるチュートリアル 原著第2版
- 作者: John K. Kruschke,前田和寛,小杉考司
- 出版社/メーカー: 共立出版
- 発売日: 2017/07/22
- メディア: 大型本
- この商品を含むブログを見る

StanとRでベイズ統計モデリング (Wonderful R)
- 作者: 松浦健太郎,石田基広
- 出版社/メーカー: 共立出版
- 発売日: 2016/10/25
- メディア: 単行本
- この商品を含むブログ (8件) を見る

- 作者: 清水裕士
- 出版社/メーカー: ナカニシヤ出版
- 発売日: 2014/10/01
- メディア: 単行本
- この商品を含むブログを見る

- 作者: Richard McElreath
- 出版社/メーカー: Chapman and Hall/CRC
- 発売日: 2016/02/19
- メディア: ハードカバー
- この商品を含むブログを見る
第1回 Kobe.R annex(犬4匹本 輪読会)開催しました!
2017年9月24日 大阪府立大学・なんばサテライトにて Kobe.R annex 第1回を開催しました。第1部『ベイズ統計モデリング―R,JAGS,Stanによるチュートリアル― 原著第2版』の輪読,第2部 分析ネタなんでもという構成でした。参加者は5名(+会場をご提供いただいた大阪府立大学の先生)。

予定は第6章〜9章の予定だったのですが,8章までとしました。もちろん全員,犬4匹本を購入済みです。以下,輪読会の簡単メモです。
第7章
- JAGS の情報が載っていてわかりやすいウェブサイトがある。
http://ecological-stats.com/tag/jags/
- MCMCスライド集
追加情報: 警告メッセージ: 命令 ''/Library/Frameworks/R.framework/Resources/bin/R' CMD config CXX 2>/dev/null' の実行は状態 69 を持ちました
追加情報: 警告メッセージ: 命令 '/Library/Frameworks/R.framework/Resources/bin/R CMD SHLIB file8dae4ce1404e.cpp 2> file8dae4ce1404e.cpp.err.txt' の実行は状態 1 を持ちました
疑問点
- Gelman-Rubin統計量(184頁)はRハットのことだろうか?
→どうやらそのようです。
- 間引き(thinning)はすべき? すべきでない?
→犬4匹本は基本thinningしない的な立場(191頁)のようだが,thinning したほうがよいという文献もあるらしい。
- thinning をした場合,サンプリング時間はどう変わるだろうか?
→あるモデルで「iteration 1000,thin 1」「iteration 1000,thin 2」「iteration 2000,thin 2」を stan で実行してみると,90秒・90秒・180秒となった。保存されたオブジェクトのデータは8MB, 4MB, 8MB。thinning の設定でサンプリング時間は変わらないが,保存されるオブジェクトの容量は変わる。
第8章
- 参加者の方が8章の便利関数をパッケージ化されました!
参加させていただき、ありがとうございました。
— ヨゼ (@kyusque) 2017年9月24日
8章の便利コマンドですが、パッケージとしてgithubに上げました。
devtools::install_github("kyusque/DBDA2E-utilities", args = "--no-multiarch")
LT枠(分析ネタなんでも)
状態空間モデルについて
共変量バランシング傾向スコアを使った統計的因果推論について
以上です。次回もいずれ開催したいと思います。
大きい iPad Pro で論文を快適に読む方法
自分の中でだいたい固めることができたので、大きい iPad Pro で快適に論文を読む方法を書いておきます。最近、質的研究ばかりやっていて、R とかあんまり触っていないため、こういうネタしかないんです。
結論から
まず先に結論を言うと、2017年9月20日現在、次の組み合わせが私にはピッタリです。
1. iPad Pro 12.9インチ
2. アップルペンシル
3. アップルペンシルのキャップ紛失防止ツール
4. 適度に滑りにくくするための保護シート
5. PDF Expert
6. スリーブケース
私の電子リーダー端末遍歴
タブレットやスマホはいろいろ触ってきましたが、論文を読むに関しては、Retina ディスプレイの iPad(第3世代)→ソニーのデジタルペーパー(旧モデル・DPT-S1)→ 小さい iPad Pro(9.7インチ・2015年モデル)→大きい iPad Pro(12.9インチ・2017年モデル)とたどってきました。他にもKindleとかソニーのリーダーとかでもチャレンジしましたが、目には優しいものの動作が重くダメでした。
なぜ紙で論文を読まないのか?
私が紙で論文を読みたくないと思ったのは単純に「かさばるから」です。仕事柄出張が多く(昨年は224泊)、論文をたくさん持ち歩きたくありません。社会科学の論文は(少なくとも私の領域では)だいたい1本20ページくらいで、5本でA4・100ページ、10本で200ページ。出張で持ち歩くには思ったよりかさばるんです…。そのため電子化しかないと数年前からいろいろ工夫していました。
中には論文は「紙で読む派」という方もいらっしゃると思いますが、差し迫った問題がなければ、私はどちらでもいいと思います。お好きなほうを選べばいいです。
デジタルペーパー VS 小さいiPad Pro VS 大きい iPad Pro
電子化された論文を読む勝ちパターンがこの1年で固まりました。まず昨年、ソニーデジタルペーパー(DPT-S1)を大阪のソニーストアで実機を確認。さすがに定価で買うには抵抗があり、中古をヤフオクでゲット。それでもそれなりのお値段がしました。
デジタルペーパーのいいところ
○ 軽い、薄い。
○ なんか目に優しい感じがする。
○ 基本、読み書きに特化しているので、論文読みに集中できる。
デジタルペーパーのイマイチだったところ
△ 動作がもったり(新モデルは改善しているそうです)
△ 文字がギザギザで読みにくい(これも新モデルでは改善しているそうです)
△ 思ったよりペンが引っかかる。もっと滑らかなのが個人的には好き。
△ 英語論文を読んでいて、知らない単語が出てきたとき、別の端末で調べる必要がある。
△ 論文を読んでいて調べ物をしたい場合、ネットで快適に調べることができない。
数ヶ月ほど使って「ナンカチガウ」感が出てきて、だんだんと使わなくなっていきました。「これではあんまり論文が読めないなぁ」と困り、iPad Pro はどうだろうと思い立ちました。iPad Pro には大きいサイズ(12.9インチ)と小さいサイズ(当時9.7インチだった)があります。
大きい iPad Pro を仕事に使っている知人がいたので見せてもらって、ちょっと大きいかなと思ったので、小さい iPad Pro を使うことに決め、アップルの整備済製品で購入しました。お得です。
小さい iPad Pro のいいところ
○ 字がきれい。
○ 知らない英単語が出てきたとき、付属の英語辞書ですぐわかる。
○ wi-fi につなげて、快適に調べ物ができる。
○ アップルペンシルはなかなかいい感じ。
iPad の辞書機能は特に便利です。私は英語に不自由しているので、よく知らない単語が出てきます。これを他の電子辞書を使わずに、iPad 内蔵の辞書で調べることができるのでストレスがとても減り、QOLアップ。
PDFを読むとき、PDF Expert を使うのですが、上のように知らない単語を選択して「定義」をタップすれば、内蔵辞書ですぐに意味を確認できます。超便利!
アップルペンシルの書き心地は動画では伝わりにくいですが、こんな感じ。
小さい iPad Pro のイマイチなところ
△ 使っていると、だんだん小さく感じてくる。
△ ケースに入れて使っていると、思ったより重く感じる。
△ アップルペンシルはいいけど、ちょっと滑りすぎる。
また半年ほど使って、また「ナンカチガウ」感が出てきたので、大きい iPad Pro を本格検討。新型の大きい iPad が出て、かなり迷いました。清水の舞台から飛び降りる気持ちで移行を決意。在庫があるなら全国どのアップルストアにも行く(出張ついでに)覚悟でした。
結果、銀座にアップルストアにあったので、すぐにゲット。そして現在に至ります。まだそんなに経っていないですけど、とても満足して使っています。
大きい iPad Pro のいいところ
○ 小さい iPad Pro のいいところは全部ある。
○ さらに画面が大きく、見やすい。
大きい iPad Pro のイマイチなところ
△ デカい。
大きい iPad Pro をより快適に使う方法
以下、より楽しく、快適に iPad Pro 12.9 インチを使って論文を読むために試した方法を書きます。
アップルペンシルのキャップカバー(必須)
まずアップルペンシルは必須です。しかし、アップルペンシルの最大の弱点はキャップ。小さい iPad Pro を使っているときにアップルペンシルはすでに活用していましたが、すぐにキャップをなくしました。
キャップがなくても普通に使えますが、なんかカッコ悪い。仕方がないので、大きい iPad Pro 導入時にキャップだけ再度購入しました。アップルストアで修理扱いです。修理の予約が必要だし、修理代は1000円くらい。
また紛失したら悲しいので、キャップカバーを導入。修理代より安いので、導入したほうがいいです。どのキャップカバーでも構いません。

- 出版社/メーカー: LENSEN
- メディア: エレクトロニクス
- この商品を含むブログを見る
ちょっと不格好なのですが、紛失のリスクを考えて、ここはガマンですかね。
ペーパーライク保護フィルム(必須)
ソニーデジタルペーパーと比べ、iPad Pro はツルッツルです。そのためアップルペンシルが滑りすぎます。多少の引っかかりが必要なため、ディスプレイが紙のような感じになる「ペーパーライク保護フィルム」を導入しました。

エレコム 2017年新型 iPad Pro 12.9 / 2015年発売 iPad pro 12.9 液晶保護フィルム ペーパーライク 反射防止 TB-A17LFLAPL
- 出版社/メーカー: エレコム
- 発売日: 2017/06/07
- メディア: Personal Computers
- この商品を含むブログを見る
最近は安いのが出ているので、好きなのを選べばいいかと思います。ただ、気をつけてほしいことがあります。それは、せっかくの美麗なディスプレイが台無しになることです。
画面はちょっとざらついた見た目になりますし、指紋はむっちゃ付着します。きれいな画像・映像を見たい人にはガマンできないと思います。
しかし、この iPad Pro は論文を読むためにあるのです! 割り切ってエンタメは諦めましょう…。次第に目は慣れていきます。なんか違和感のある手触りも慣れます。ざらつきはありますが、画面はヌルヌル動くので、操作は問題ありません。
PDFリーダー(必須。お好きなのを)
先ほど書いたように、PDF Expert を使っています。他のPDFリーダーも試して、いちばんしっくりきたためです。かなり感覚的でちゃんとした理由はありません。ドロップボックスに読むべき論文のフォルダを作り、そのフォルダと PDF Expert を同期させます。

格安SIM(お好きにどうぞ)
wi-fi でつながっていないときに(電車の中とか)で論文を読んでいて、ネットで調べ物をしたいときに便利です。ただ、つい余計なものを見てしまうときもあるので、導入するかどうかは好き好きで。私は楽天ポイント(ホテル手配は楽天トラベルだからけっこう貯まる)で支払える楽天SIMにしています。
アンテナが2本しか立っていなかったのでスピードが少し遅いですね。大きな問題はないです。
スリーブケース(お好きにどうぞ)
ケースは重いので、スリーブケースにしました。デスクにどかんと置いて使うか、手に持って使うだけなので、別に立てて使うことはないからです。アマゾンとかで好きなモノを選んでください。
私は純正品を使っていますが、キャップ付きのアップルペンシルだと収まりが悪く、ちょっとカッコわるいです。

というわけで、大きい iPad Pro であなたも快適な論文読みライフを送りませんか? コスパには目をつむってになりますけど…。
第1回 Kobe.R 別館を開催します!

来る2017年9月24日に Kobe.R の弟分的な存在の勉強会「Kobe.R annex(別館)」第1回を開催します。小さく、緩く(いい意味で)、楽しくやっていきたいと思います。2部制にして、第1部は『ベイズ統計モデリング: R,JAGS, Stanによるチュートリアル 原著第2版』(犬4匹本)を輪読します。第2部では、初心者セッションおよびLT大会です。第1部から参加、もしくは第2部のみ参加をお選びいただけます。
参加者数は最大11名と小さいため、LT枠などが埋まらない場合は、参加者同士で時間の許す限りR関連の話題やRを使った研究ネタについて(アイデアレベルでも)と話し合おうと思っています。初心者セッションは “R for Datascience” または “Quantitative Social Science: An Introduction” を題材にしてもいいかな~とも思っています。
日曜の大阪・難波での開催です。すでに滋賀県から参加される方もいらっしゃいます。関西在住の方(もちろんその他の地域の方も)は奮ってご参加ください!
