階層モデルでロバストな推定を試す

【追記】
「外れ値の確認」の項目を追記しました。

---

　
以前『データ分析をマスターする〜』の9章を階層モデルを使って分析しました。しかし，ちょっと気になることがあったので，再分析してみます。なお，本エントリーは Stan Advent Calendar 2017 の9日目です。

　
今回主に使うパッケージは次の2つです。

library(tidyverse)
library(brms)
library(rethinking)
# devtools::install_github("rmcelreath/rethinking",ref="Experimental")  # 必要であれば。

　
使用したデータは『データ分析をマスターする〜』のサポートサイトにありますが，使って見るならちゃんと買ったほうがいいかなぁと思います（私は買って読んでます）。 　
　

以前の分析の課題　〜外れ値の存在〜

　
この前は都道府県別の女性労働力率と合計特殊出生率のデータを使って，シンプソンのパラドックスをベイズ推定を使った階層モデル（マルチレベル分析）でどう解消するか考えました。↓がこの前のエントリーです。

hikaru1122.hatenadiary.jp

　
データの特徴は「全体で見ると負の相関だけど，年代別（1980年と2000年）で見ると正の相関が出る」というものです。散布図を再掲します。

　

　
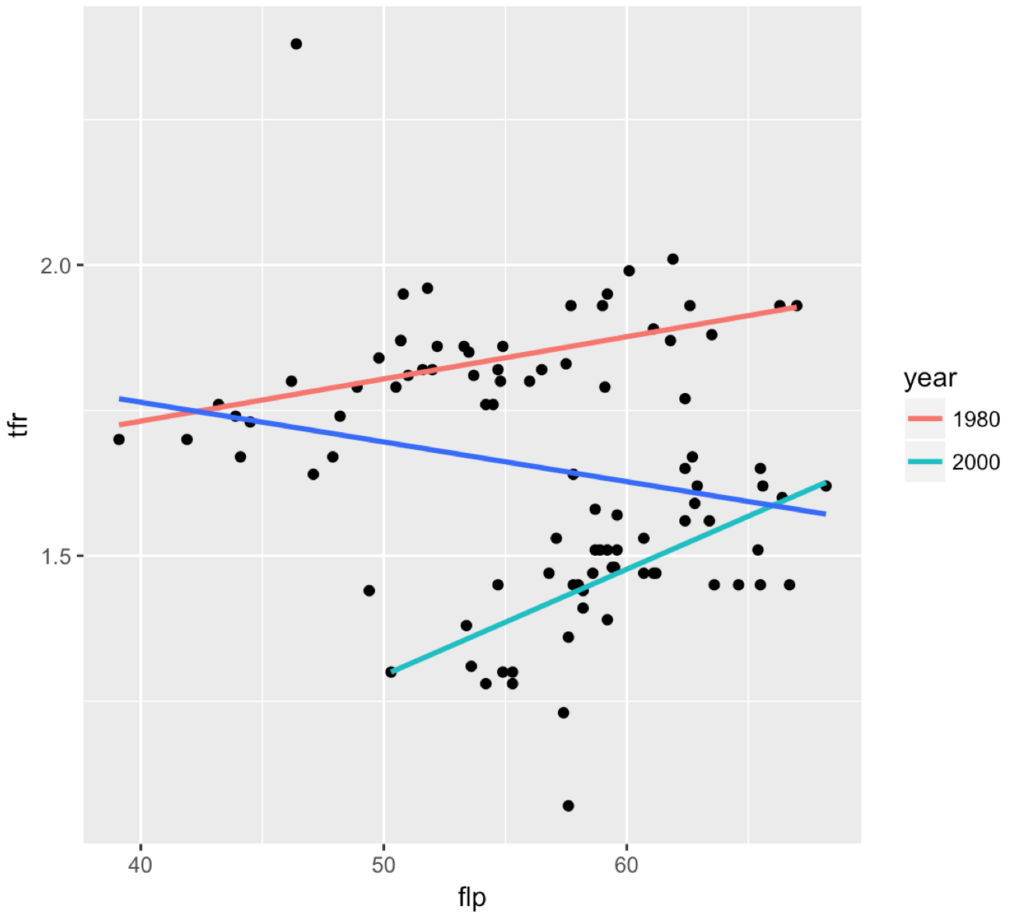
前回，傾きはほぼ同じだから，変量効果は切片だけ考えました。それはいいのですが，気になっていて見なかったことにしようとしたことが1つ。外れ値の存在です。

ggplot(d, aes(x=factor(year), y=tfr)) + geom_boxplot(aes(fill=factor(year))) + 
geom_jitter() + coord_flip() + 
theme(legend.position = "none")

　

　
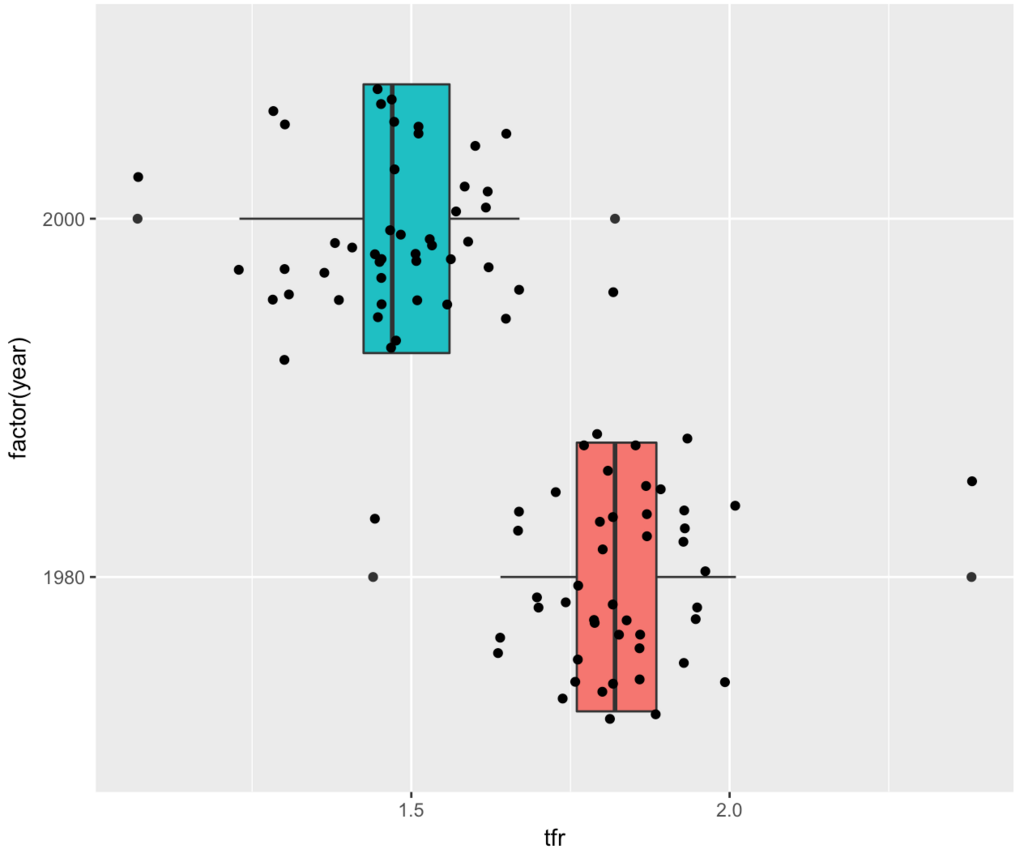
上図を見ると，各年代で合計特殊出生率の極端に高い都道府県と極端に低い都道府県が存在します。下表から、どの年代も最大値は沖縄（都道府県コード47）で，最小値は東京都（都道府県コード13）です。

library(knitr) # kable() で下の表を作るためにマークダウン出力用
d %>% group_by(year) %>% 
summarise(max(tfr), which.max(tfr), min(tfr), which.min(tfr)) %>% kable()

year	min(tfr)	which.min(tfr)	max(tfr)	which.max(tfr)
1980	1.44	13	2.38	47
2000	1.07	13	1.82	47

外れ値の確認

　
外れ値が存在するときは t 分布を使うとよいと犬4匹本に書いてあります（466ページ）ので，以下，ｔ分布を使った外れ値があるデータにも対応できるロバストな分析を行います。

　
ところで、今回のケースが外れ値といえるのか少し確かめたいと思います。外れ値を調べるために Smirnov-Grubbs 検定（すみるのふぐらぶす）があります。この検定はデータが正規分布から発生している仮定しています。しかし、今回はｔ分布から発生すると考えていきたいので、自由度46（=47-1）のｔ分布の95％信頼区間を見て判断してみます。

t = abs(qt(0.05/2, 47-1))
SE1980 = sd(d$tfr[d$yearID==1])/sqrt(47)
SE2000 = sd(d$tfr[d$yearID==2])/sqrt(47)

> # 1980年の下側
> mean(d$tfr[d$yearID==1]) - t*SE1980
[1] 1.789009
> # 1980年の上側
> mean(d$tfr[d$yearID==1]) + t*SE1980
[1] 1.868012
> # 2000年の下側
> mean(d$tfr[d$yearID==2]) - t*SE2000
[1] 1.433888
> # 2000年の上側
> mean(d$tfr[d$yearID==2]) + t*SE2000
[1] 1.512069

　
1980年の95％信頼区間は1.79〜1.87，2000年の95％信頼区間は1.43〜1.51でした。よって，外れ値が存在すると言えそうです。上記の計算はこちらを参考にしました。

www2.hak.hokkyodai.ac.jp

t 分布を使ったロバストな推定

ロバストとは？

　
ロバストとは「頑健」という意味です。外れ値があっても，データのメインボディの中心やばらつきなどを妥当に推定する方法を「ロバスト推定」と言います（藤澤 2017）。

　
ｔ分布には3つのパラメータがあります。自由度ν（にゅー），中心μ（みゅー），スケールσ（しぐま）です。μやσは平均と標準偏差の記号として使われますが，ここではｔ分布なので平均ではなく中心 center，標準偏差ではなくスケール scale と書きました（BDA3, 437ページ）。

　
t 分布の感じをつかむには Unadon さんのこちらのエントリーがわかりやすいです。

mrunadon.github.io

　
Stan のおすすめ事前分布を見ると，t（3, 0, 1）のようですが，上の箱ひげ図を見ると幅広そうなので，今回はできるだけ幅が広く，裾が長いｔ分布の t（1, 0, 10）でやってみます。なお，BDA3には「自由度が1や2のｔ分布はあんまり現実的ではない」とありますが，今回は実験ということで目をつぶります（437ページ）。

　
Stan おすすめ事前分布についてはこちらの説明があります。

github.com

　
Stan のコードは自前では書けませんので，今回も brms パッケージを使います。変量効果は前と同じ（半コーシー分布に従っている）。単回帰分析なので，切片とflpの傾きがｔ分布に従っていると考えます。モデルのイメージは下のような感じ（かっこいいグラフィカルな表現はできなかった）。

　

　
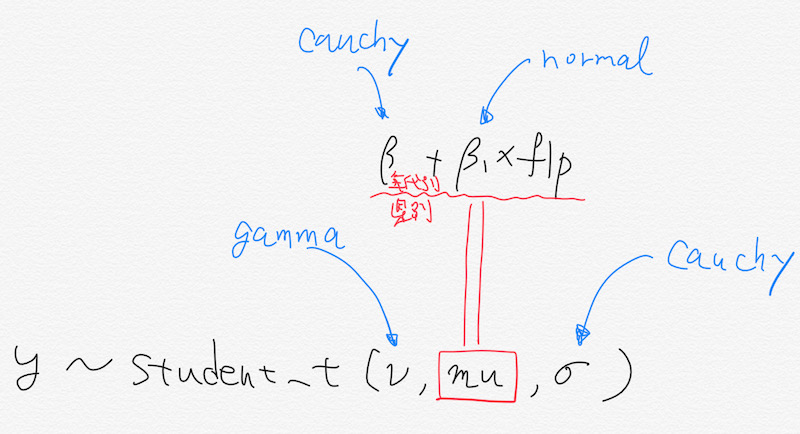
コードは次のとおりです。

library(brms)
options(mc.cores = parallel::detectCores())

prior2 = c(set_prior("cauchy(0, 3)", class = "sd", group = "prefID"),
           set_prior("cauchy(0, 3)", class = "sd", group = "yearID"),
           set_prior("student_t(1,0,10)", class = "b"),
           set_prior("student_t(1,0,10)", class = "Intercept"))

kekka2 = brm(tfr ~ 1 + flp + (1 | prefID) + (1 | yearID), data = d, iter = 5000, 
             family = "student", prior = prior2,
             control = list(adapt_delta = 0.9, max_treedepth = 15))

　
ちゃんと指定した事前分布になっているかコードを確認します。

> stancode(kekka2)
（中略）

  // priors including all constants 
  target += student_t_lpdf(b | 1,0,10);  ←ココ
  target += student_t_lpdf(temp_Intercept | 1,0,10);  ←ココ
  target += student_t_lpdf(sigma | 3, 0, 10)
    - 1 * student_t_lccdf(0 | 3, 0, 10); 
  target += gamma_lpdf(nu | 2, 0.1)
    - 1 * gamma_lccdf(1 | 2, 0.1); 
  target += cauchy_lpdf(sd_1 | 0, 3) ←ココ
    - 1 * cauchy_lccdf(0 | 0, 3); 
  target += normal_lpdf(z_1[1] | 0, 1); 
  target += cauchy_lpdf(sd_2 | 0, 3) ←ココ
    - 1 * cauchy_lccdf(0 | 0, 3); 
  target += normal_lpdf(z_2[1] | 0, 1); 

（後略）

分析結果

　
分析結果は次のとおりです。無事収束して，心なしか有効サンプルサイズが増えたようです。また前回と違って切片の固定効果は0をまたがなくなり，最後の警告の数は減りました。都道府県の変量効果と傾きの固定効果がほぼ0なのは同じです。

> kekka2
 Family: student(identity) 
Formula: tfr ~ 1 + flp + (1 | prefID) + (1 | yearID) 
   Data: d (Number of observations: 94) 
Samples: 4 chains, each with iter = 5000; warmup = 2500; thin = 1; 
         total post-warmup samples = 10000
    ICs: LOO = NA; WAIC = NA; R2 = NA
 
Group-Level Effects: 
~prefID (Number of levels: 47) 
              Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sd(Intercept)     0.13      0.02     0.09     0.17       1183 1.01

~yearID (Number of levels: 2) 
              Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sd(Intercept)     0.96      0.82     0.15     3.11       1162 1.00

Population-Level Effects: 
          Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
Intercept     1.67      0.69     0.22     3.16       1287 1.00
flp          -0.00      0.00    -0.01     0.01        829 1.00

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sigma     0.04      0.01     0.03     0.05       1538 1.00
nu       13.89     11.73     2.69    46.47       5153 1.00

Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample 
is a crude measure of effective sample size, and Rhat is the potential 
scale reduction factor on split chains (at convergence, Rhat = 1).
 警告メッセージ: 
There were 7 divergent transitions after warmup. Increasing adapt_delta above 0.9 may help.
See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup 
> 

　
警告メッセージについては，divergent transitions の数が小さいのと Rhat を見ると収束しているので無視します（アヒル本176ページ）。

　
傾きは前回と同じように変量効果も固定効果も0に近いです。切片の変量効果が減ってしまっています（前のモデルが1.22）が，切片の固定効果の95％信用区間は0をまたがなくなりました（切片の有効サンプルサイズも増えています）。図で確認します（太い線が50％信用区間，細い線が90％信用区間です。点は事後中央値）。

　

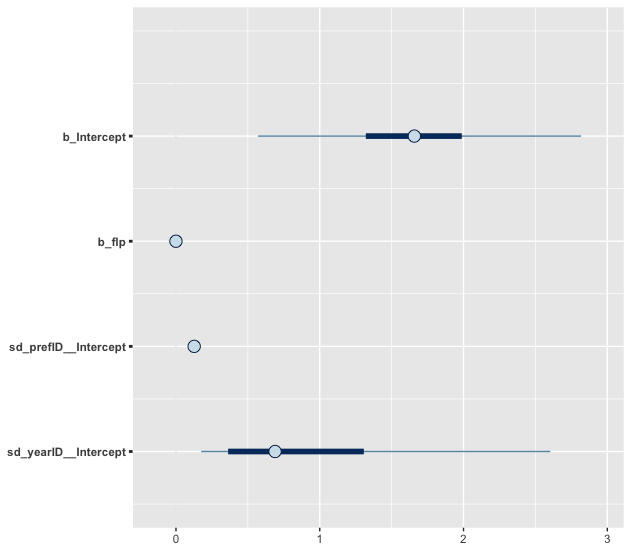
モデル比較

　
WAIC は前回のモデルに及びませんでした。残念。

> waic(kekka1, kekka2)
                   WAIC    SE
kekka1          -268.04 16.62
kekka2          -260.81 18.53
kekka1 - kekka2   -7.23  3.47

まとめ

　
今回は「外れ値があるので，ロバストな推定をしよう」とチャレンジしてきました。結果はイマイチで，たった94行のデータに適用するのはあんまり意味がないのでしょう。しかし，いつもと違った事前分布に触れることができました。また Stan コードが書けなくても，パッケージで比較的に Stan に触れられる例にもなったかなと思います。

　
間違いなどがあれば，ぜひお教えください🙏
いつかお会いする機会があれば🍣を進呈いたします。

参考にした書籍

以下，今回，参考にした書籍です。どれも難しいですね…。

データ分析をマスターする12のレッスン (有斐閣アルマBasic)

ロバスト統計: 外れ値への対処の仕方 (ISMシリーズ:進化する統計数理)

ベイズ統計モデリング: R,JAGS, Stanによるチュートリアル 原著第2版

StanとRでベイズ統計モデリング (Wonderful R)

Bayesian Data Analysis, Third Edition (Chapman & Hall/CRC Texts in Statistical Science)

Statistical Rethinking: A Bayesian Course with Examples in R and Stan (Chapman & Hall/CRC Texts in Statistical Science)